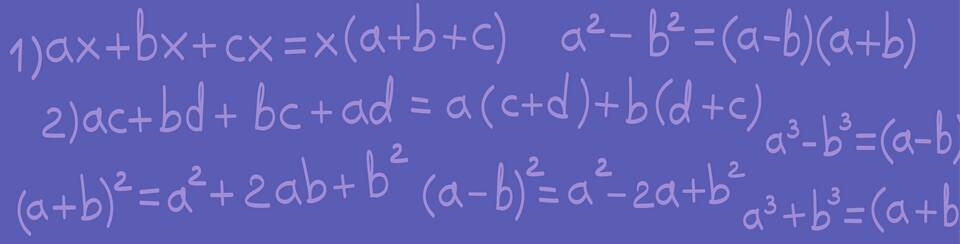Сумма многочленов - это операция в алгебре, результатом которой является новый многочлен, полученный путем сложения соответствующих членов исходных многочленов. Эта операция является одной из основных при работе с полиномами и широко применяется в различных разделах математики.
Содержание
Основные понятия
| Термин | Определение |
| Многочлен (полином) | Алгебраическая сумма одночленов |
| Одночлен | Произведение числового коэффициента и переменных в степенях |
| Степень многочлена | Наибольшая степень переменной в многочлене |
Правила сложения многочленов
Для сложения многочленов необходимо:
- Раскрыть скобки (если они есть)
- Привести подобные слагаемые
- Записать результат в стандартной форме
Примеры сложения многочленов
Пример 1: Простые многочлены
Сложим многочлены: P(x) = 3x² + 2x - 5 и Q(x) = x² - 4x + 1
| Шаг 1 | (3x² + 2x - 5) + (x² - 4x + 1) |
| Шаг 2 | 3x² + x² + 2x - 4x - 5 + 1 |
| Шаг 3 | 4x² - 2x - 4 |
Пример 2: Многочлены разной степени
Сложим: A(x) = 2x³ + x и B(x) = 5x² - 3
| Результат | 2x³ + 5x² + x - 3 |
Свойства суммы многочленов
Операция сложения многочленов обладает следующими свойствами:
- Коммутативность: P(x) + Q(x) = Q(x) + P(x)
- Ассоциативность: (P(x) + Q(x)) + R(x) = P(x) + (Q(x) + R(x))
- Существование нулевого элемента: P(x) + 0 = P(x)
- Существование противоположного многочлена: P(x) + (-P(x)) = 0
Степень суммы многочленов
Степень суммы многочленов не превышает наибольшей из степеней слагаемых:
| Случай | Степень суммы |
| Степени равны | ≤ максимальной степени |
| Степени различны | Равна наибольшей степени |
Геометрическая интерпретация
Сумма многочленов может быть представлена графически как сложение соответствующих ординат графиков функций:
- Для каждой точки x вычисляются значения P(x) и Q(x)
- Значения складываются
- Строится новый график по полученным точкам
Применение суммы многочленов
Операция сложения многочленов используется в:
- Аппроксимации функций
- Решение систем уравнений
- Теории кодирования
- Компьютерной графике
- Физическом моделировании
Особые случаи
| Случай | Результат |
| Сложение с нулевым многочленом | Исходный многочлен |
| Сложение противоположных многочленов | Нулевой многочлен |
| Сложение симметричных многочленов | Новый симметричный многочлен |
Понимание операции сложения многочленов является фундаментальным для дальнейшего изучения алгебры и ее приложений в различных областях науки и техники.